Originating with Aristotle, term logic was the dominant form of logic used till the the late nineteenth century. It reasons on the basis of the relationships between categories (referred to as terms).
I. Categorical Terms
The basic unit in categorical syllogistic logic is the categorical term. Categorical terms are simply the placing of things or concepts into distinct classes or categories based on some specified characteristics. Each categorical term divides the world into those things included in the category and those things not included.
II. Categorical Propositions
With categorical terms we can build categorical propositions. A Categorical propositions is a statement with two categorical terms which asserts some relationship between them.
There are four parts to a categorical proposition. In standard form, the first term in the statement is referred to as the subject term (the term which we are saying something about) and the second as the predicate term. The relationship between the subject and predicate terms is described through the use of a copula and quantifier. The copula (also referred to as quality) denotes either an affirmative/inclusive relationship (are) or negative/exclusive (are not) relationship. The quantifier provides how much of the subject term relates to the predicate term by use of universal quantifiers (all, none), and particular quantifiers (some).
A model categorical proposition can be represented as:
Quantifier [subject term] copula [predicate term]
So with the example All men are mortal; the word All is the quantifier, men is the subject term, are is the copula and mortal is the predicate term.
There are four types of categorical propositions:
A: Universal Affirmative
All S are P
E: Universal Negative
No S are P
I: Particular Affirmative
Some S are P
O: Particular Negative
Some S are not P
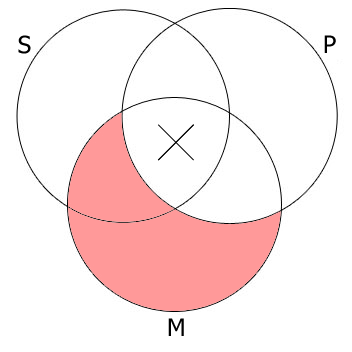
Here are the four categorical propositions illustrated with Venn Diagrams:
III. Categorical Syllogisms
Combining categorical propositions, we create categorical syllogisms. A categorical syllogism is a syllogistic argument consisting of three categorical propositions (two premises and a conclusion) and three categorical terms, each of which is used twice.
There are a total of 256 possible varieties of categorical syllogisms but only 15 are valid (per Boolean logic). Two important valid categorical syllogisms are:
BARBARA, AAA-1
1. All M are P
2. All S are M
3. Therefore all S are P
DARII, AII-1
1. All M are P
Here is a link to a page which lists all 15 valid categorical syllogisms along with their corresponding Venn diagrams.
The validity of a categorical syllogism can be determined by either applying a set of rules or through the use of Venn diagrams. Here are two links which expand on the subject"
-The six necessary conditions for valid categorical syllogisms
-Testing validity using Venn diagrams
Santa Barbara City College: Philosophy-111 Critical Thinking And Writing: The 15 Valid Syllogistic Forms
Society for Positive Philosophy and Interdisciplinary Studies (SPPIS): A Classroom Introduction to Logic: Nature of Proposition
II. Categorical Propositions
With categorical terms we can build categorical propositions. A Categorical propositions is a statement with two categorical terms which asserts some relationship between them.
There are four parts to a categorical proposition. In standard form, the first term in the statement is referred to as the subject term (the term which we are saying something about) and the second as the predicate term. The relationship between the subject and predicate terms is described through the use of a copula and quantifier. The copula (also referred to as quality) denotes either an affirmative/inclusive relationship (are) or negative/exclusive (are not) relationship. The quantifier provides how much of the subject term relates to the predicate term by use of universal quantifiers (all, none), and particular quantifiers (some).
A model categorical proposition can be represented as:
Quantifier [subject term] copula [predicate term]
So with the example All men are mortal; the word All is the quantifier, men is the subject term, are is the copula and mortal is the predicate term.
There are four types of categorical propositions:
A: Universal Affirmative
All S are P
E: Universal Negative
No S are P
I: Particular Affirmative
Some S are P
O: Particular Negative
Some S are not P
Here are the four categorical propositions illustrated with Venn Diagrams:
 |
III. Categorical Syllogisms
Combining categorical propositions, we create categorical syllogisms. A categorical syllogism is a syllogistic argument consisting of three categorical propositions (two premises and a conclusion) and three categorical terms, each of which is used twice.
There are a total of 256 possible varieties of categorical syllogisms but only 15 are valid (per Boolean logic). Two important valid categorical syllogisms are:
BARBARA, AAA-1
1. All M are P
2. All S are M
3. Therefore all S are P
DARII, AII-1
1. All M are P
Here is a link to a page which lists all 15 valid categorical syllogisms along with their corresponding Venn diagrams.
The validity of a categorical syllogism can be determined by either applying a set of rules or through the use of Venn diagrams. Here are two links which expand on the subject"
-The six necessary conditions for valid categorical syllogisms
-Testing validity using Venn diagrams
Santa Barbara City College: Philosophy-111 Critical Thinking And Writing: The 15 Valid Syllogistic Forms
Society for Positive Philosophy and Interdisciplinary Studies (SPPIS): A Classroom Introduction to Logic: Nature of Proposition

I can not reach 15 valid syllogistic forms and their Venn diagrams
ReplyDelete